（本小题满分12分）
已知函数f(x)=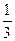
x3+
ax2+ax-2(a∈R),
(1)若函数f(x)在区间(-∞，+∞)上为单调增函数，求实数a的取值范围；
(2)设A(x1,f(x1))、B(x2,f(x2))是函数f(x)的两个极值点，若直线AB的斜率不小于-
，求实数a的取值范围.
相关试题
中，
.
，求数列
的通项公式；
求证：
.
的图象经过点
，且在
处的切线方程是
.
的解析式；
中，
=1，
，其中实数
.
；
求证：
推荐套卷
（本小题满分12分）
已知函数f(x)=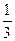x3+ax2+ax-2(a∈R),
(1)若函数f(x)在区间(-∞，+∞)上为单调增函数，求实数a的取值范围；
(2)设A(x1,f(x1))、B(x2,f(x2))是函数f(x)的两个极值点，若直线AB的斜率不小于-，求实数a的取值范围.
粤公网安备 44130202000953号