某公司是否对某一项目投资,由甲、乙、丙三位决策人投票决定.他们三人都有“同意”、“中立”、“反对”三类票各一张.投票时,每人必须且只能投一张票,每人投三类票中的任何一类票的概率都为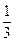 ,他们的投票相互没有影响.规定:若投票结果中至少有两张“同意”票,则决定对该项目投资;否则,放弃对该项目投资.
,他们的投票相互没有影响.规定:若投票结果中至少有两张“同意”票,则决定对该项目投资;否则,放弃对该项目投资.
(Ⅰ)求此公司决定对该项目投资的概率;
(Ⅱ)记投票结果中“中立”票的张数为随机变量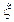 ,求
,求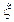 的分布列及数学期望E
的分布列及数学期望E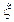 .
.
相关知识点
推荐套卷
某公司是否对某一项目投资,由甲、乙、丙三位决策人投票决定.他们三人都有“同意”、“中立”、“反对”三类票各一张.投票时,每人必须且只能投一张票,每人投三类票中的任何一类票的概率都为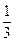 ,他们的投票相互没有影响.规定:若投票结果中至少有两张“同意”票,则决定对该项目投资;否则,放弃对该项目投资.
,他们的投票相互没有影响.规定:若投票结果中至少有两张“同意”票,则决定对该项目投资;否则,放弃对该项目投资.
(Ⅰ)求此公司决定对该项目投资的概率;
(Ⅱ)记投票结果中“中立”票的张数为随机变量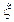 ,求
,求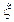 的分布列及数学期望E
的分布列及数学期望E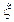 .
.