甲、乙两位学生参加数学竞赛培训，在培训期间，他们参加的5次预赛成绩记录如下：
甲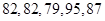 
乙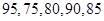 
（1）用茎叶图表示这两组数据；
（2）从甲、乙两人的成绩中各随机抽取一个，求甲的成绩比乙高的概率；
（3）①求甲、乙两人的成绩的平均数与方差，②若现要从中选派一人参加数学竞赛，根据你的计算结果，你认为选派哪位学生参加合适？
、
都是非零向量，且向量
与
垂直，
与
垂直，求
、
、
两两所成的角相等，并且
，
，
，求向量
的长度。
中，求
的值．推荐套卷
甲、乙两位学生参加数学竞赛培训，在培训期间，他们参加的5次预赛成绩记录如下：
甲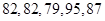
乙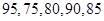
（1）用茎叶图表示这两组数据；
（2）从甲、乙两人的成绩中各随机抽取一个，求甲的成绩比乙高的概率；
（3）①求甲、乙两人的成绩的平均数与方差，②若现要从中选派一人参加数学竞赛，根据你的计算结果，你认为选派哪位学生参加合适？
粤公网安备 44130202000953号