(本小题满分13分)
已知,在水平平面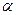 上有一长方体
上有一长方体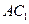 绕
绕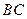 旋转
旋转 得到如图所示的几何体.
得到如图所示的几何体.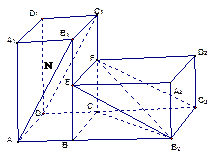
(Ⅰ)证明:平面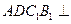 平面
平面 ;
;
(Ⅱ)当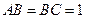 时,直线
时,直线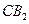 与平面
与平面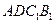 所成的角的正弦值为
所成的角的正弦值为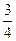 ,求
,求 的长度;
的长度;
(Ⅲ)在(Ⅱ)条件下,设旋转过程中,平面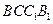 与平面
与平面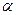 所成的角为
所成的角为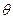 ,
, 长方体
长方体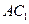 的最高点离平面
的最高点离平面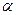 的距离为
的距离为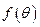 ,请直接写出
,请直接写出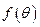 的一个表达式,并注明定义域.
的一个表达式,并注明定义域.
推荐套卷
(本小题满分13分)
已知,在水平平面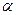 上有一长方体
上有一长方体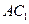 绕
绕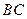 旋转
旋转 得到如图所示的几何体.
得到如图所示的几何体.
(Ⅰ)证明:平面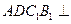 平面
平面 ;
;
(Ⅱ)当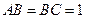 时,直线
时,直线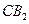 与平面
与平面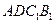 所成的角的正弦值为
所成的角的正弦值为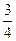 ,求
,求 的长度;
的长度;
(Ⅲ)在(Ⅱ)条件下,设旋转过程中,平面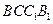 与平面
与平面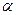 所成的角为
所成的角为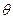 ,
, 长方体
长方体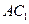 的最高点离平面
的最高点离平面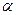 的距离为
的距离为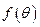 ,请直接写出
,请直接写出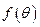 的一个表达式,并注明定义域.
的一个表达式,并注明定义域.