（本小题满分12分）
在△ABC中，a、b、c分别是角A、B、C的对边，且（2a＋c）cosB＋bcosC＝0．
（Ⅰ）求角B
的值；
（Ⅱ）已知函数f（x）＝2cos（2x－B），将f（x）的图象向左平移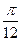
后得到函数g（x）的图象，求g（x）的单调增区间．
，
，
，
．当
，
，
，
时，分别求点
的坐标．
，0）（ ）距离之比为
的点的轨迹，求此曲线的方程，并判断曲线的形状。
相外切，并且与直线
：
相切于点P（3，
），求此圆C的方程。
轴切于点（5，0）并在
轴上截取弦长为10的圆的方程。
上任意一点P（ ），不等式
恒成立，求实数
的取值范围。推荐套卷
（本小题满分12分）
在△ABC中，a、b、c分别是角A、B、C的对边，且（2a＋c）cosB＋bcosC＝0．
（Ⅰ）求角B的值；
（Ⅱ）已知函数f（x）＝2cos（2x－B），将f（x）的图象向左平移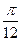后得到函数g（x）的图象，求g（x）的单调增区间．
粤公网安备 44130202000953号