(本小题满分12分)
投到“时尚生活”杂志的稿件,先由两位初审专家进行评审,若能通过两位初审专家的评审,则予以录用;若两位初审专家都未通过,则不予录用;若恰能通过一位初审专家的评审,则再由第三位专家进行复审,若能通过复审专家的评审,则予以录用,否则,不予录用.设稿件能通过各初审专家评审的概率均为0.5, 复审的稿件能通过评审的概率为0.3,各位专家独立评审.
复审的稿件能通过评审的概率为0.3,各位专家独立评审.
(1)求投到该杂志的1篇稿件被录用的概率.
(2)若某人投到该杂志3篇稿件,求他被录用稿件篇数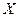 的分布列及期望值.
的分布列及期望值.
推荐套卷
(本小题满分12分)
投到“时尚生活”杂志的稿件,先由两位初审专家进行评审,若能通过两位初审专家的评审,则予以录用;若两位初审专家都未通过,则不予录用;若恰能通过一位初审专家的评审,则再由第三位专家进行复审,若能通过复审专家的评审,则予以录用,否则,不予录用.设稿件能通过各初审专家评审的概率均为0.5, 复审的稿件能通过评审的概率为0.3,各位专家独立评审.
复审的稿件能通过评审的概率为0.3,各位专家独立评审.
(1)求投到该杂志的1篇稿件被录用的概率.
(2)若某人投到该杂志3篇稿件,求他被录用稿件篇数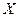 的分布列及期望值.
的分布列及期望值.