(本题满分12分) 在九江市教研室组织的一次优秀青年教师联谊活动中,有一个有奖竞猜的环节.主持人准备了A、B两个相互独立的问题,并且宣布:幸运观众答对问题A可获奖金1000元,答对问题B可获奖金2000元,先答哪个题由观众自由选择,但只有第一个问题答对,才能再答第二题,否则终止答题.若你被选为幸运观众,且假设你答对问题A、B的概率分别为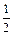 、
、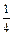 .
.
(1) 记先回答问题A的奖金为随机变量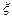 , 则
, 则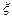 的取值分别是多少?
的取值分别是多少?
(2) 你觉得应先回答哪个问题才能使你获得更多的奖金?请说明理由.
相关知识点
推荐套卷

 时,求函数
时,求函数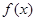 的极值;
的极值;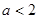 时,讨论函数
时,讨论函数 |≤ 2;命题
|≤ 2;命题 .若
.若 是
是 的必要而不充分条件,求实数
的必要而不充分条件,求实数 的取值范围.
的取值范围.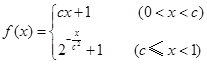 满足
满足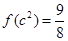 .
. 的值;
的值; 成立的
成立的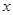 的取值范围.
的取值范围.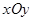 上绘制的一列抛物线和一列直线,在焦点为
上绘制的一列抛物线和一列直线,在焦点为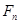 的抛物线列
的抛物线列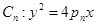 中,
中,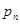 是首项和公比都为
是首项和公比都为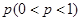 的等比数列,过
的等比数列,过 与
与 相交于
相交于 和
和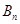 (
(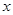 轴的上方,
轴的上方, 的斜率是定值;
的斜率是定值; 、
、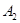 、
、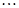 、
、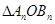 的面积为
的面积为 ,证明:数列
,证明:数列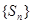 是等比数列,并求所有这些三角形的面积的和.
是等比数列,并求所有这些三角形的面积的和.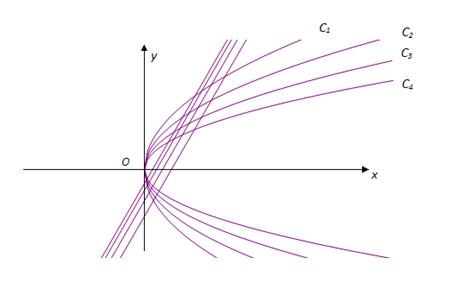
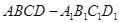 中, 侧棱
中, 侧棱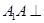 底面
底面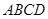 ,
,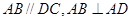 ,
,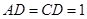 ,
, ,
,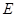 为棱
为棱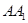 的中点.
的中点. 
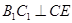 ;
;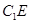 与
与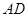 所成角的大小.(结果用反三角函数值表示)
所成角的大小.(结果用反三角函数值表示) 粤公网安备 44130202000953号
粤公网安备 44130202000953号