如图,平面ABEF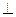
ABCD,四边形ABEF与ABCD都是直角梯形, 
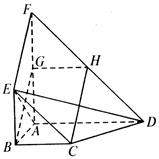
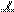
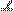
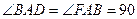°，BC 
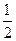AD,BE 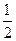FA,G、H分别为FA、FD的中点．
（1）证明四边形BCHG是平行四边行．
（2）C、D、E、F四点是否共面?为什么?
（3）设AB=BE,证明平面ADE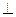平面CDE．
的最小值。
的最小值。
且
，关于
的不等式
的解集是
，解关于
的解集。
，若不等式
的解集为
，试解关于t的不等式
。
.推荐套卷
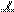
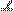
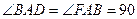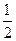如图,平面ABEFABCD,四边形ABEF与ABCD都是直角梯形, °，BC AD,BE 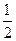FA,G、H分别为FA、FD的中点．
（1）证明四边形BCHG是平行四边行．
（2）C、D、E、F四点是否共面?为什么?
（3）设AB=BE,证明平面ADE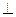平面CDE．
粤公网安备 44130202000953号