已知椭圆C的左，右焦点坐标分别为
,离心率是
。椭圆C的左，右顶点分别记为A,B。点S是椭圆C上位于
轴上方的动点，直线AS,BS与直线
分别交于M,N两点。
（1） 求椭圆C的方程；
（2） 求线段MN长度的最小值；
（3） 当线段MN的长度最小时，在椭圆C上的T满足：T到直线AS的距离等于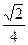
.
试确定点T的个数。
相关试题
(a+b)三向量的终点在同一条直线上？
=a，
=b，
=c，试用a、b、c表示
，
，
+
.
km的C、D两点，并测得∠ACB=75°，∠BCD=45°，∠ADC=30°，∠ADB=45°，求A、B之间的距离.
，
求
；（2）证明
在
是增函数(14分)
，求圆心到直线
的距离的取值范围.(14分)推荐套卷
已知椭圆C的左，右焦点坐标分别为,离心率是。椭圆C的左，右顶点分别记为A,B。点S是椭圆C上位于轴上方的动点，直线AS,BS与直线分别交于M,N两点。
（1） 求椭圆C的方程；
（2） 求线段MN长度的最小值；
（3） 当线段MN的长度最小时，在椭圆C上的T满足：T到直线AS的距离等于.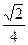
试确定点T的个数。
粤公网安备 44130202000953号