(本小题满分12分)
如图1,在平面内,ABCD边长为2的正方形,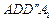 和
和 都是正方形。将两个正方形分别沿AD,CD折
都是正方形。将两个正方形分别沿AD,CD折 起,使
起,使 与
与 重合于点D1。设直线l过点B且垂直于正方形ABCD所在的平面,点E是直线l上的一个动点,且与点D1位于平面A
重合于点D1。设直线l过点B且垂直于正方形ABCD所在的平面,点E是直线l上的一个动点,且与点D1位于平面A BCD同侧,设
BCD同侧,设 (图2)。
(图2)。

(1)设二面角E – AC – D1的大小为q,当 时,求
时,求 的余弦值;
的余弦值;
(2)当 时在线段
时在线段 上是否存在点
上是否存在点 ,使平面
,使平面 平面
平面 ,若存在,求出
,若存在,求出 分
分 所成的比
所成的比 ;若不存在,请说明理由。
;若不存在,请说明理由。
推荐套卷
(本小题满分12分)
如图1,在平面内,ABCD边长为2的正方形,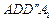 和
和 都是正方形。将两个正方形分别沿AD,CD折
都是正方形。将两个正方形分别沿AD,CD折 起,使
起,使 与
与 重合于点D1。设直线l过点B且垂直于正方形ABCD所在的平面,点E是直线l上的一个动点,且与点D1位于平面A
重合于点D1。设直线l过点B且垂直于正方形ABCD所在的平面,点E是直线l上的一个动点,且与点D1位于平面A BCD同侧,设
BCD同侧,设 (图2)。
(图2)。

(1)设二面角E – AC – D1的大小为q,当 时,求
时,求 的余弦值;
的余弦值;
(2)当 时在线段
时在线段 上是否存在点
上是否存在点 ,使平面
,使平面 平面
平面 ,若存在,求出
,若存在,求出 分
分 所成的比
所成的比 ;若不存在,请说明理由。
;若不存在,请说明理由。