甲、乙两人各射击3次,甲每次击中目标的概率为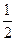 ,乙每次击中目标的概率为
,乙每次击中目标的概率为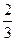 ,
,
(1)记甲击中目标的次数为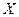 ,求随机变量
,求随机变量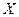 的概率分布表及数学期望
的概率分布表及数学期望 ;
;
(2)求乙至多击中目标2次的概率;
(3)求甲恰好比乙多击中目标2次的概率.
相关知识点
推荐套卷
甲、乙两人各射击3次,甲每次击中目标的概率为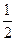 ,乙每次击中目标的概率为
,乙每次击中目标的概率为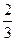 ,
,
(1)记甲击中目标的次数为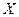 ,求随机变量
,求随机变量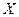 的概率分布表及数学期望
的概率分布表及数学期望 ;
;
(2)求乙至多击中目标2次的概率;
(3)求甲恰好比乙多击中目标2次的概率.