对定义在区间l，上的函数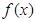
，若存在开区间
和常数C，使得对任意的
都有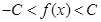
，且对任意的x
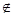（a，b）都有
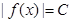恒成立，则称函数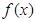为区间I上的“Z型”函数．
（I）求证：函数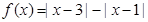
是R上的“Z型”函数；
（Ⅱ）设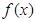是（I）中的“Z型”函数，若不等式
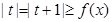对任意的x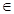
R恒成立，求实数t的取值范围．
相关试题
上，求圆心为C的圆的标准方程。
中，
、
为底面圆的两条直径，
，且
，
，
为
的中点.
与
所成角的正切值.
)，求该几何体的表面积和体积. 
的前
项和记作
，满足
，
．
求出数列
，且
对正整数
的范围；
证明：
中不可能有等差子数列（已知
。相关知识点
推荐套卷
对定义在区间l，上的函数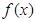，若存在开区间和常数C，使得对任意的都有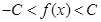，且对任意的x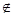（a，b）都有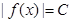恒成立，则称函数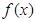为区间I上的“Z型”函数．
（I）求证：函数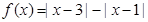是R上的“Z型”函数；
（Ⅱ）设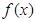是（I）中的“Z型”函数，若不等式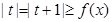对任意的x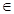R恒成立，求实数t的取值范围．
粤公网安备 44130202000953号