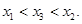定义：已知函数f（x）与g（x），若存在一条直线y="kx" +b，使得对公共定义域内的任意实数均满足g（x）≤f（x）≤kx+b恒成立，其中等号在公共点处成立，则称直线y="kx" +b为曲线f（x）与g（x）的“左同旁切线”．已知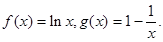
（I）证明：直线y=x-l是f（x）与g（x）的“左同旁切线”；
（Ⅱ）设P（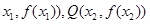
是函数 f（x）图象上任意两点，且0<x1<x2，若存在实数x3>0，使得
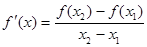．请结合（I）中的结论证明：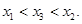
相关试题
满足：
.
，求数列
的前n项和
.
asinC－ccosA.
满足
，且
成等比数列。
；
为数列
的前n项和
。
的定义域及最小正周期；
.
的单调性；
.如果对任意
，
，求
的取值范围.推荐套卷
定义：已知函数f（x）与g（x），若存在一条直线y="kx" +b，使得对公共定义域内的任意实数均满足g（x）≤f（x）≤kx+b恒成立，其中等号在公共点处成立，则称直线y="kx" +b为曲线f（x）与g（x）的“左同旁切线”．已知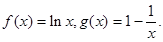
（I）证明：直线y=x-l是f（x）与g（x）的“左同旁切线”；
（Ⅱ）设P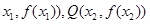（是函数 f（x）图象上任意两点，且0<x1<x2，若存在实数x3>0，使得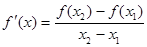．请结合（I）中的结论证明：
粤公网安备 44130202000953号