(本 题满分13分)
题满分13分)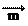 在△ABC中,角A、B、C所对的边分别为a、b、c,且CosA=
在△ABC中,角A、B、C所对的边分别为a、b、c,且CosA= ,向量 =
,向量 = ,
,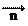
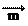
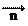 =
= ,且 ⊥
,且 ⊥
(1)求角C的值;
(2)求sinB的值;
(3)若c=5,求△ABC的面积。
相关知识点
推荐套卷
(本 题满分13分)
题满分13分)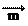 在△ABC中,角A、B、C所对的边分别为a、b、c,且CosA=
在△ABC中,角A、B、C所对的边分别为a、b、c,且CosA= ,向量 =
,向量 = ,
,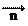
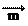
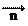 =
= ,且 ⊥
,且 ⊥
(1)求角C的值;
(2)求sinB的值;
(3)若c=5,求△ABC的面积。