某商场经销某商品,根据以往资料统计,顾客采用的付款期数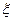 的分布列为
的分布列为
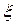 |
1 |
2 |
3 |
4 |
5 |
 |
0.4 |
0.2 |
0.2 |
0.1 |
0.1 |
商场经销一件该商品,采用1期付款,其利润为200元;分二期或3期付款,其利润为250元;分4期或5期付款,其利润为300元。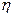 表示经销一件该商品的利润.
表示经销一件该商品的利润.
(1)求事件A:“购买该商品的3位顾客中,至少有1位采用1期付款”的概率.
(2)求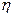 的分布列及期望.
的分布列及期望.
推荐套卷
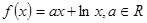
 的极值;
的极值; ,如果存在曲线上的点
,如果存在曲线上的点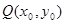 ,且
,且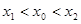 ,使得曲线在点
,使得曲线在点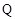 处的切线
处的切线 ∥
∥ ,则称
,则称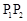 的伴随切线。特别地,当
的伴随切线。特别地,当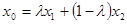 ,
,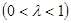 时,又称
时,又称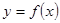 的任意一条弦均有伴随切线,并且伴随切线是唯一的;
的任意一条弦均有伴随切线,并且伴随切线是唯一的; 伴随切线?若存在,给出一条这样的曲线 ,并证明你的结论; 若不存在 ,说明理由。
伴随切线?若存在,给出一条这样的曲线 ,并证明你的结论; 若不存在 ,说明理由。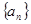 中,数列的前
中,数列的前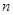 项和
项和 满足
满足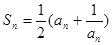 .
.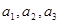 ;
;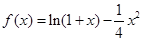 在区间
在区间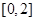 上的最大值和最小值.
上的最大值和最小值.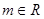 ,复数z =
,复数z =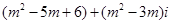 .
.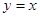 上?
上? 粤公网安备 44130202000953号
粤公网安备 44130202000953号