（（本小题满分12分）
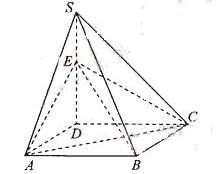
如图，四棱锥S＝ABCD的底面是正方形，SD⊥平面ABCD,SD＝AD＝a,点E是SD上的点，且DE＝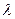
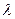a(0<≦1). 
(Ⅰ)求证：对任意的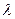
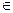（0、1），都有AC⊥BE:
(Ⅱ)若二面角C-AE-D的大小为600C，求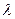的值。
相关试题
中，
分别是
所对的边，
,
，三角形的面积为
，
的大小；（2）求
的值．
的值；（2）若
垂直，求
的值．
为偶函数．
的值；
有且只有一个根，求实数
的取值范围．
．
在
上是增函数，求实数
的取值范围；
上的最小值为3，求实数
(
)
均为实数，且
，
，
求证：推荐套卷
（（本小题满分12分）
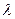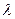如图，四棱锥S＝ABCD的底面是正方形，SD⊥平面ABCD,SD＝AD＝a,点E是SD上的点，且DE＝a(0<≦1). (Ⅰ)求证：对任意的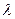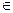（0、1），都有AC⊥BE:
(Ⅱ)若二面角C-AE-D的大小为600C，求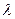的值。
粤公网安备 44130202000953号