已知动点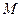 到定点
到定点 的距离与到定直线
的距离与到定直线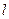 :
: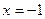 的距离相等,点C在直线
的距离相等,点C在直线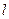 上。
上。
(1)求动点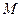 的轨迹方程。
的轨迹方程。
(2)设过定点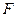 ,且法向量
,且法向量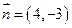 的直线与(1)中的轨迹相交于
的直线与(1)中的轨迹相交于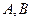 两点且点
两点且点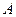 在
在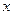 轴的上方。判断
轴的上方。判断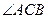 能否为钝角并说明理由。进一步研究
能否为钝角并说明理由。进一步研究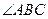 为钝角时点
为钝角时点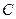 纵坐标的取值范围。
纵坐标的取值范围。
相关知识点
推荐套卷
已知动点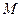 到定点
到定点 的距离与到定直线
的距离与到定直线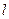 :
: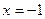 的距离相等,点C在直线
的距离相等,点C在直线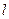 上。
上。
(1)求动点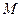 的轨迹方程。
的轨迹方程。
(2)设过定点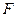 ,且法向量
,且法向量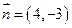 的直线与(1)中的轨迹相交于
的直线与(1)中的轨迹相交于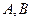 两点且点
两点且点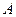 在
在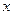 轴的上方。判断
轴的上方。判断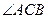 能否为钝角并说明理由。进一步研究
能否为钝角并说明理由。进一步研究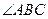 为钝角时点
为钝角时点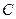 纵坐标的取值范围。
纵坐标的取值范围。