等差数列{ }中,
}中, +
+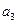 +
+ =-
=- 12, 且
12, 且  ·
·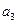 ·
· ="80." 且公差
="80." 且公差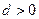 求:
求:
(1)通项公式 及前n项和
及前n项和
(2)若在 每相邻两项中间插入一个新的数得到一个新的数列记为{
每相邻两项中间插入一个新的数得到一个新的数列记为{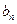 },求
},求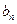 的前n项和
的前n项和 .
.
相关知识点
推荐套卷
等差数列{ }中,
}中, +
+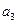 +
+ =-
=- 12, 且
12, 且  ·
·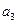 ·
· ="80." 且公差
="80." 且公差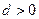 求:
求:
(1)通项公式 及前n项和
及前n项和
(2)若在 每相邻两项中间插入一个新的数得到一个新的数列记为{
每相邻两项中间插入一个新的数得到一个新的数列记为{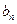 },求
},求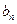 的前n项和
的前n项和 .
.