设函数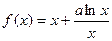
，其中
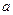为常数．
（Ⅰ）证明：对任意
，
的图象恒过定点；
（Ⅱ）当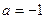
时，判断函数是否存在极值？若存在，求出极值；若不存在，说明理由；
（Ⅲ）若对任意
时，恒为定义域上的增函数，求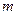
的最大值．
请考生在第22、23、24题中任选一题做答，如果多做，则按所做的第一题记分.
相关试题
，曲线
在点
处的切线方程为
。
，
的值；
，且
时，
，求
的取值范围。
恒成立，求m的取值范围
满足：
，
，
．
及；
(n
N*)，求数列
的前n项和
．
且
,且△ABC的面积为
,求a＋b的值
推荐套卷
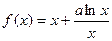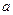设函数，其中为常数．
（Ⅰ）证明：对任意，的图象恒过定点；
（Ⅱ）当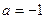时，判断函数是否存在极值？若存在，求出极值；若不存在，说明理由；
（Ⅲ）若对任意时，恒为定义域上的增函数，求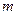的最大值．
请考生在第22、23、24题中任选一题做答，如果多做，则按所做的第一题记分.
粤公网安备 44130202000953号