定义:如果数列 的任意连续三项均能构成一个三角形的三边长,则称
的任意连续三项均能构成一个三角形的三边长,则称 为“三角形”数列.对于“三角形”数
为“三角形”数列.对于“三角形”数 列
列 ,如果函数
,如果函数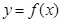 使得
使得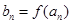 仍为一个“三角形”数列,则称
仍为一个“三角形”数列,则称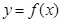 是数列
是数列 的“保三角形函数”,
的“保三角形函数”,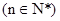 .
.
(Ⅰ)已知 是首项为2,公差为1的等差数列,若
是首项为2,公差为1的等差数列,若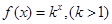 是数列
是数列 的“保三角形函数”,求k的取值范围;
的“保三角形函数”,求k的取值范围;
(Ⅱ)已知数列 的首项为2010,
的首项为2010,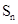 是数列
是数列 的前n项和,且满足
的前n项和,且满足 ,证明
,证明 是“三角形”数列;
是“三角形”数列;
(Ⅲ)根据“保三角形函数”的定义,对函数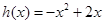 ,
, ,和数列1,
,和数列1,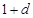 ,
,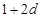 ,(
,( )提出一个正确的命题,并说明理由.
)提出一个正确的命题,并说明理由.
推荐套卷
定义:如果数列 的任意连续三项均能构成一个三角形的三边长,则称
的任意连续三项均能构成一个三角形的三边长,则称 为“三角形”数列.对于“三角形”数
为“三角形”数列.对于“三角形”数 列
列 ,如果函数
,如果函数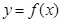 使得
使得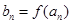 仍为一个“三角形”数列,则称
仍为一个“三角形”数列,则称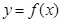 是数列
是数列 的“保三角形函数”,
的“保三角形函数”,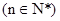 .
.
(Ⅰ)已知 是首项为2,公差为1的等差数列,若
是首项为2,公差为1的等差数列,若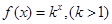 是数列
是数列 的“保三角形函数”,求k的取值范围;
的“保三角形函数”,求k的取值范围;
(Ⅱ)已知数列 的首项为2010,
的首项为2010,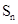 是数列
是数列 的前n项和,且满足
的前n项和,且满足 ,证明
,证明 是“三角形”数列;
是“三角形”数列;
(Ⅲ)根据“保三角形函数”的定义,对函数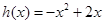 ,
, ,和数列1,
,和数列1,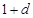 ,
,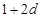 ,(
,( )提出一个正确的命题,并说明理由.
)提出一个正确的命题,并说明理由.