某校选拔若干名学生组建数学奥林匹克集训队,要求选拔过程分前 后两次进行,当第一次选拔合格后方可进入第二次选拔,两次选拔过程相互独立。根据甲、乙、丙三人现有的水平,第一次选拔,甲、乙、丙三人合格的概率依次为
后两次进行,当第一次选拔合格后方可进入第二次选拔,两次选拔过程相互独立。根据甲、乙、丙三人现有的水平,第一次选拔,甲、乙、丙三人合格的概率依次为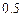 ,
,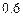 ,
,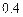 。第二次选拔,甲、乙、丙三人合格的概率依次为
。第二次选拔,甲、乙、丙三人合格的概率依次为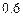 ,
,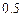 ,
,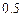 。
。
(1)求第一次选拔后甲、乙两人中只有甲合格的 概
概 率;
率;
(2)分别求出甲、乙、丙三人经过前后两次选拔后合格的概率;
(3)求甲、乙、丙经过前后两次选拔后,恰有一人合格的概率。
推荐套卷
某校选拔若干名学生组建数学奥林匹克集训队,要求选拔过程分前 后两次进行,当第一次选拔合格后方可进入第二次选拔,两次选拔过程相互独立。根据甲、乙、丙三人现有的水平,第一次选拔,甲、乙、丙三人合格的概率依次为
后两次进行,当第一次选拔合格后方可进入第二次选拔,两次选拔过程相互独立。根据甲、乙、丙三人现有的水平,第一次选拔,甲、乙、丙三人合格的概率依次为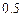 ,
,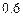 ,
,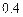 。第二次选拔,甲、乙、丙三人合格的概率依次为
。第二次选拔,甲、乙、丙三人合格的概率依次为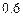 ,
,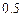 ,
,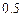 。
。
(1)求第一次选拔后甲、乙两人中只有甲合格的 概
概 率;
率;
(2)分别求出甲、乙、丙三人经过前后两次选拔后合格的概率;
(3)求甲、乙、丙经过前后两次选拔后,恰有一人合格的概率。