如图
，某货轮在A处看灯塔B在货轮的北偏东
，距离为
海里，在A处看灯塔C在货轮的北偏西
，距离为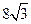
海里。货轮由A处向正北方向航行到D处时，再看灯塔B在南偏东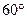
(1) A处与D处的距离；
(2) 灯塔C处与D处的距离。
相关试题
，首项
，前
项和为
，且
，
，
成等差数列．
的前
．
中
平面
，点
在棱
上，且
，底面为直角梯形，
分别是
的中点．
// 平面
；
与底面
的三内角
的对边分别为 
．
，
，若
的大小．
，
，且△
，求角
的取值范围．
．
，求实数
的取值范围；
的最大值．
．
；
的解集．相关知识点
推荐套卷
如图，某货轮在A处看灯塔B在货轮的北偏东，距离为海里，在A处看灯塔C在货轮的北偏西，距离为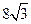海里。货轮由A处向正北方向航行到D处时，再看灯塔B在南偏东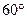
(1) A处与D处的距离；
(2) 灯塔C处与D处的距离。
粤公网安备 44130202000953号