(本小题满分12分)
某人向一目标射击，在
处射击一次击中目标的概率为
，击中目标得2分；在
处射击一次击中目标的概率为
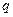，击中目标得1分.若他射击三次，第一次在处射击，后两次都在
处射击，用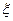
表示他3次射击后得的总分，其分布列为：
|
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
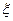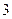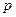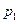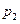⑴求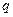及的数学期望
；
⑵求此人3次都选择在处向目标射击且得分高于2分的概率.
的定义域为
求实数
的取值范围。
的定义域为
，且
=
对于任意的实数
都恒成立．若已知
试求
的值
的定义域为自然数集，且满足条件
，及
=1，求
的定义域为
，求函数
的定义域。
是
且
试用
相关知识点
推荐套卷
(本小题满分12分)
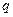某人向一目标射击，在处射击一次击中目标的概率为，击中目标得2分；在处射击一次击中目标的概率为，击中目标得1分.若他射击三次，第一次在处射击，后两次都在处射击，用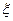表示他3次射击后得的总分，其分布列为：
|
|
|
|
|
|
|
|
|
|
|
|
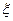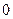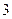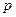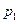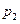⑴求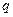及的数学期望；
⑵求此人3次都选择在处向目标射击且得分高于2分的概率.
粤公网安备 44130202000953号