(本大题满分12分)
一个容器的盖子用一个正四棱台和一个球焊接而成,球的半径为R,正四棱台的上、下底面边长分别为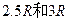 ,斜高为
,斜高为
(1)求这个容器盖子的表面积(用R表示,焊接处对面积的影响忽略不记);
(2)若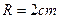 ,为盖子涂色时所用的涂料每
,为盖子涂色时所用的涂料每 可以涂
可以涂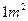 ,问100个这样的盖子约需涂料多少
,问100个这样的盖子约需涂料多少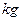 (精确到
(精确到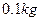 )?
)?
推荐套卷
(本大题满分12分)
一个容器的盖子用一个正四棱台和一个球焊接而成,球的半径为R,正四棱台的上、下底面边长分别为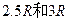 ,斜高为
,斜高为
(1)求这个容器盖子的表面积(用R表示,焊接处对面积的影响忽略不记);
(2)若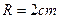 ,为盖子涂色时所用的涂料每
,为盖子涂色时所用的涂料每 可以涂
可以涂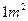 ,问100个这样的盖子约需涂料多少
,问100个这样的盖子约需涂料多少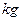 (精确到
(精确到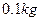 )?
)?