设椭圆C1：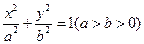
的左、右焦点分别是F1、F2，下顶点为A，线段OA的中点为B（O为坐标原点），如图．若抛物线C2：
与y轴的交点为B，且经过F1，F2点．
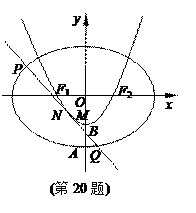
（Ⅰ）求椭圆C1的方程；
（Ⅱ）设M（0，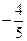
），N为抛物线C2上的一动点，过点N作抛物线C2的切线交椭圆C1于P、Q两点，求
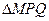面积的最大值．
相关试题
.
不可能为偶函数；
上单调递减的充要条件是
.
中，
，
分别是
的中点，且
.
与
所成角的大小；
与平面
所成角的正弦值.
中，
，
，设
.
时，求
的值；
，求
的值.
满足
，
.
；
，记不等式
的解集为
.
时，求集合
，求实数
的取值范围.推荐套卷
设椭圆C1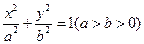：的左、右焦点分别是F1、F2，下顶点为A，线段OA的中点为B（O为坐标原点），如图．若抛物线C2：与y轴的交点为B，且经过F1，F2点．
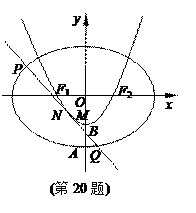
（Ⅰ）求椭圆C1的方程；
（Ⅱ）设M（0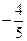，），N为抛物线C2上的一动点，过点N作抛物线C2的切线交椭圆C1于P、Q两点，求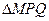面积的最大值．
粤公网安备 44130202000953号