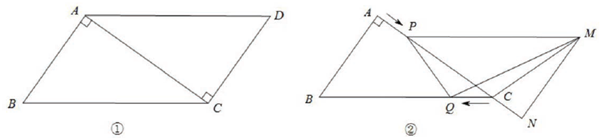
(本小题满分12分)
已知:如图①,在□ABCD中, AB=3cm,BC=5cm.AC⊥AB。△ACD沿AC的方向匀速平移得到△PNM,速度为1cm/s;同时,点Q从点C出发,沿CB方向匀速运动,速度为1cm/s,当△PNM停止平移时,点Q也停止运动.如图②,设运动时间为t(s)(0<t<4).解答下列问题:
(1)当t为何值时,PQ∥MN?
(2)设△QMC的面积为y(cm2),求y与t之间的函数关系式;
(3)是否存在某一时刻t,使S△QMC∶S四边形ABQP=1∶4?若存在,求出t的值;若不存在,请说明理由.
(4)是否存在某一时刻t,使PQ⊥MQ?若存在,求出t的值;若不存在,请说明理由.