(本小题满分14分)设不等式组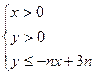 所表示的平面区域为
所表示的平面区域为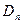 ,记
,记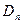 内的格点(格点即横坐标和纵坐标均为整数的点)个数为
内的格点(格点即横坐标和纵坐标均为整数的点)个数为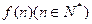
(1)求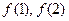 的值及
的值及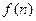 的表达式;(2)记
的表达式;(2)记 ,试比较
,试比较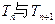 的大小;若对于一切的正整数
的大小;若对于一切的正整数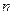 ,总有
,总有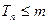 成立,求实数
成立,求实数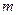 的取值范围;
的取值范围;
(3)设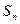 为数列
为数列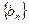 的前
的前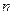 项的和,其中
项的和,其中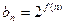 ,问是否存在正整数
,问是否存在正整数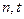 ,使
,使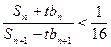 成立?若存在,求出正整数
成立?若存在,求出正整数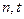 ;若不存在,说明理由。
;若不存在,说明理由。
推荐套卷
(本小题满分14分)设不等式组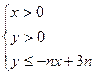 所表示的平面区域为
所表示的平面区域为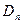 ,记
,记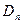 内的格点(格点即横坐标和纵坐标均为整数的点)个数为
内的格点(格点即横坐标和纵坐标均为整数的点)个数为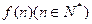
(1)求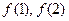 的值及
的值及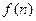 的表达式;(2)记
的表达式;(2)记 ,试比较
,试比较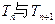 的大小;若对于一切的正整数
的大小;若对于一切的正整数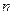 ,总有
,总有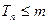 成立,求实数
成立,求实数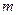 的取值范围;
的取值范围;
(3)设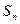 为数列
为数列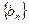 的前
的前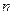 项的和,其中
项的和,其中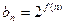 ,问是否存在正整数
,问是否存在正整数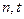 ,使
,使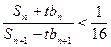 成立?若存在,求出正整数
成立?若存在,求出正整数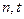 ;若不存在,说明理由。
;若不存在,说明理由。