（本小题满分12分）
如图：已知△PAB所在的平面与菱形ABCD所在的平面垂直，且PA＝PB＝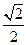
AB，∠ABC＝60°，E为AB的中点．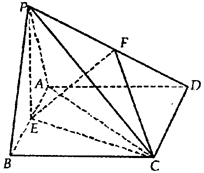 
（Ⅰ）证明：CE⊥PA；
（Ⅱ）若F为线段PD上的点，且EF与平面PEC的
夹角为45°,求平面EFC与平面PBC夹角的
余弦值．
，试用含
的式子表示
．
，
，求证：
．
，求这个三角形的顶角的正弦、余弦及正切值．
中，
，
，求
的值．
，
，求证：
．推荐套卷
（本小题满分12分）
如图：已知△PAB所在的平面与菱形ABCD所在的平面垂直，且PA＝PB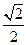＝AB，∠ABC＝60°，E为AB的中点．
（Ⅰ）证明：CE⊥PA；
（Ⅱ）若F为线段PD上的点，且EF与平面PEC的
夹角为45°,求平面EFC与平面PBC夹角的
余弦值．
粤公网安备 44130202000953号