(本小题满分12分)
已知函数f(x)=x2-ax+b (a,b∈R)的图像经过坐标原点,且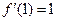 ,数列{
,数列{ }的前n项和
}的前n项和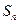 =f(n)(n∈N*).
=f(n)(n∈N*).
(Ⅰ) 求数列{ }的通项公式;(Ⅱ)若数列{
}的通项公式;(Ⅱ)若数列{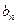 }满足
}满足 +
+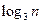 =
=  ,求数列{
,求数列{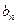 }的前n项和.
}的前n项和.
相关知识点
推荐套卷
(本小题满分12分)
已知函数f(x)=x2-ax+b (a,b∈R)的图像经过坐标原点,且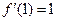 ,数列{
,数列{ }的前n项和
}的前n项和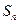 =f(n)(n∈N*).
=f(n)(n∈N*).
(Ⅰ) 求数列{ }的通项公式;(Ⅱ)若数列{
}的通项公式;(Ⅱ)若数列{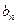 }满足
}满足 +
+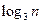 =
=  ,求数列{
,求数列{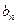 }的前n项和.
}的前n项和.