已知不垂直于x轴的动 直线l交抛物线
直线l交抛物线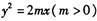 于A、B
于A、B 两点,若A,B两点满足
两点,若A,B两点满足 AQP=
AQP=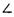 BQP,其中Q(-4,0),
BQP,其中Q(-4,0), 原点O为PQ的中点.
原点O为PQ的中点.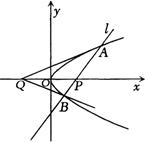
①求证A,P,B三点共线;
②当m=2时,是否存在垂直于-轴的直线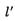 ,使
,使 得
得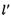 被以为直径的圆所截得的弦长为定值,如果存在,求出
被以为直径的圆所截得的弦长为定值,如果存在,求出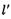 的方程,如果不存在,请说明理由
的方程,如果不存在,请说明理由
相关知识点
推荐套卷
已知不垂直于x轴的动 直线l交抛物线
直线l交抛物线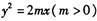 于A、B
于A、B 两点,若A,B两点满足
两点,若A,B两点满足 AQP=
AQP=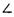 BQP,其中Q(-4,0),
BQP,其中Q(-4,0), 原点O为PQ的中点.
原点O为PQ的中点.
①求证A,P,B三点共线;
②当m=2时,是否存在垂直于-轴的直线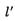 ,使
,使 得
得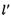 被以为直径的圆所截得的弦长为定值,如果存在,求出
被以为直径的圆所截得的弦长为定值,如果存在,求出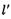 的方程,如果不存在,请说明理由
的方程,如果不存在,请说明理由