本小题满分10分)选修4-4:坐标系于参数方程
已知圆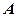 ,其圆心的极坐
,其圆心的极坐 标为
标为 ,半径为
,半径为 。
。
(Ⅰ)求过极点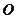 的弦的中点的轨迹方程,并说明是什么曲线;
的弦的中点的轨迹方程,并说明是什么曲线;
(Ⅱ)已知直线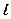 过极点
过极点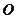 ,且极坐标方程为
,且极坐标方程为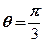 ,求圆心
,求圆心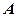 到直线
到直线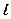 的距离。[来
的距离。[来
相关知识点
推荐套卷
本小题满分10分)选修4-4:坐标系于参数方程
已知圆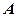 ,其圆心的极坐
,其圆心的极坐 标为
标为 ,半径为
,半径为 。
。
(Ⅰ)求过极点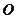 的弦的中点的轨迹方程,并说明是什么曲线;
的弦的中点的轨迹方程,并说明是什么曲线;
(Ⅱ)已知直线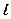 过极点
过极点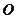 ,且极坐标方程为
,且极坐标方程为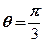 ,求圆心
,求圆心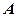 到直线
到直线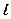 的距离。[来
的距离。[来