(本小题满分12分)
为了研究某高校大学新生的视力情况,随机地抽查了该校100名进校学生的视力情况,得到频率分布直方图如下图所示,已知后6组的频数从左到右依次是等差数列 的
的 前六项。
前六项。
(1)试确定视力介于4.9至5.0的抽查学生的人数。
(2)若规定视力低于5.0的学生属于近视 学生,试估计该校新生的近视率
学生,试估计该校新生的近视率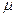 的大
的大
小。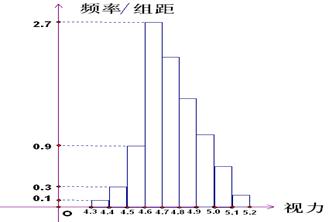
推荐套卷
(本小题满分12分)
为了研究某高校大学新生的视力情况,随机地抽查了该校100名进校学生的视力情况,得到频率分布直方图如下图所示,已知后6组的频数从左到右依次是等差数列 的
的 前六项。
前六项。
(1)试确定视力介于4.9至5.0的抽查学生的人数。
(2)若规定视力低于5.0的学生属于近视 学生,试估计该校新生的近视率
学生,试估计该校新生的近视率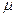 的大
的大
小。