已知中心在原点，焦点在
轴上，
离心率为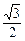
的椭圆过点（
，
)
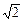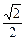（1) 求椭圆方程；
（2) 设不过原点O的直线
：
，与该椭圆交于P、Q两点，直线OP、OQ的斜率依次为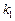
、
，满足
①求证：
为定值，并求出此定值；
②求△OPQ面积的取值范围．
相关试题
的图象上相邻
，
的终边与单位圆交于点P（
，
）.
、
、
值；
的值.
中，
，且
．
，有
．
的图象经过点
，且不等式
对一切实数
都成立．
的解析式；
，不等式
恒成立，求实数
的取值范围．
，设
．
时，求z的取值范围．推荐套卷
已知中心在原点，焦点在轴上，离心率为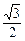的椭圆过点（，)
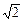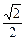（1) 求椭圆方程；
（2) 设不过原点O的直线：，与该椭圆交于P、Q两点，直线OP、OQ的斜率依次为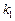、，满足
①求证：为定值，并求出此定值；
②求△OPQ面积的取值范围．
粤公网安备 44130202000953号