四、选考题:(本小题满分10分)
请考生在第22、23、题中任选一题做答,如果多做,则按所做的第一题记分.
22.选修4-4:坐标系与参数方程
已知圆O1和圆O2的极坐标方程分别为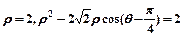
(1)把圆O1和圆O2的极坐标方程化为直角坐标方程;
(2)求经过两圆交点的直线的极坐标方程。
相关知识点
推荐套卷
四、选考题:(本小题满分10分)
请考生在第22、23、题中任选一题做答,如果多做,则按所做的第一题记分.
22.选修4-4:坐标系与参数方程
已知圆O1和圆O2的极坐标方程分别为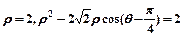
(1)把圆O1和圆O2的极坐标方程化为直角坐标方程;
(2)求经过两圆交点的直线的极坐标方程。