．甲、乙两人同时参加奥运志愿者的选拔赛，已知在备选的10道题中，甲能答对其中的6题，乙能答对其中的8题，规定每次考试都从备选题中随机抽出3题进行测试，至少答对2题才能入选．
（1）求甲答对试题数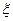
的分布列及数学期望；
（2）求甲、乙两人至少有一人入选的概率．
，求
在
的最值
，求
，求
的值
是直线
上的三点，向量
,
,
满足
解析式
次球时停止取球的概率为推荐套卷
．甲、乙两人同时参加奥运志愿者的选拔赛，已知在备选的10道题中，甲能答对其中的6题，乙能答对其中的8题，规定每次考试都从备选题中随机抽出3题进行测试，至少答对2题才能入选．
（1）求甲答对试题数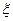的分布列及数学期望；
（2）求甲、乙两人至少有一人入选的概率．
粤公网安备 44130202000953号