如图，直线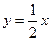
与抛物线
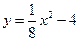，交于A,B两点，线段AB的垂直平分线与直线y+5=0交于点Q
（1）求点Q的坐标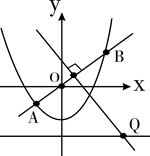
（2）当点P为抛物线上位于线段AB下方（含点A,B）的动点
时，求△OPQ面积的最
大值
相关试题
，倾斜角为
的直线L与圆
相交于A、B两点。
，求m的取值范围.
-2z
的前项和为
，已知
（
）．
的值；
是等比数列；
项，……，余下的项顺序不变，组成一个新数列
，若
项的和为
，求证：
．相关知识点
推荐套卷
如图，直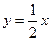线与抛物线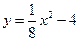，交于A,B两点，线段AB的垂直平分线与直线y+5=0交于点Q
（1）求点Q的坐标（2）当点P为抛物线上位于线段AB下方（含点A,B）的动点时，求△OPQ面积的最大值
粤公网安备 44130202000953号