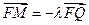椭圆的中心是原点O,它的短轴长为 ,相应于焦点F(c,0)(c>0)的准线
,相应于焦点F(c,0)(c>0)的准线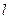 与x轴相交于点A,
与x轴相交于点A,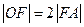 ,过点A的直线与椭圆相交于P,Q两点,
,过点A的直线与椭圆相交于P,Q两点,
(1)求椭圆的离心率及方程。
(2)若 ·
·
 ,求直线PQ的方
,求直线PQ的方 程。
程。
(3)设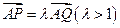 ,过点P且平行于准线l的直线与椭圆相交于另一点M,证明
,过点P且平行于准线l的直线与椭圆相交于另一点M,证明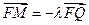
推荐套卷
椭圆的中心是原点O,它的短轴长为 ,相应于焦点F(c,0)(c>0)的准线
,相应于焦点F(c,0)(c>0)的准线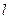 与x轴相交于点A,
与x轴相交于点A,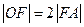 ,过点A的直线与椭圆相交于P,Q两点,
,过点A的直线与椭圆相交于P,Q两点,
(1)求椭圆的离心率及方程。
(2)若 ·
·
 ,求直线PQ的方
,求直线PQ的方 程。
程。
(3)设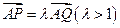 ,过点P且平行于准线l的直线与椭圆相交于另一点M,证明
,过点P且平行于准线l的直线与椭圆相交于另一点M,证明