（本小题满分12分）
甲、乙、丙三人进行某项比赛，每局有两人参加，没有平局，在一局比赛中甲胜乙的概率为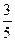
，甲胜丙的概
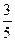，乙胜丙的概率为，比赛的规则是先由甲和乙进行第一局的比赛，然后每局的获胜者与
未参加此局比赛的人进行下一局的比赛，在比赛中，有人获胜两局就算取得比赛的胜利，比赛结束
网]
相关试题
满分12分）
，
，求
的值；（2）若
为偶函数，求
。
在区
间
上是增函数。
的定义域为集合A，
；
，求
的值；
，
，求
及
的定义域和值域均为
，求
的值。
，
， 
。
，
，
。推荐套卷
（本小题满分12分）
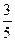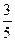甲、乙、丙三人进行某项比赛，每局有两人参加，没有平局，在一局比赛中甲胜乙的概率为，甲胜丙的概，乙胜丙的概率为，比赛的规则是先由甲和乙进行第一局的比赛，然后每局的获胜者与未参加此局比赛的人进行下一局的比赛，在比赛中，有人获胜两局就算取得比赛的胜利，比赛结束网]
粤公网安备 44130202000953号