(本小题共12分）（注意:在试题卷上作答无效）
已知抛物线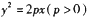
上一动点P，抛物线内一点A(3,2) ,F为焦点且
的最小值为
.
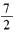(1)求抛物线的方程以
及使得
取最小值时的P点坐标；
(2)过（1)中的P点作两条互相垂直的直线与抛物线分别交于C、D两点，直线CD是否过一定点？若是，求出该定点的坐标,若不是，请说明理由.
相关试题
＝a，
＝b，试用a，b表示
.
＝
＝
，记
＝a，
＝b，求证：
＝
(b－a)．
＝a，
＝b，试用a、b表示
和
.
在[2，5]上的最大值和最小值相关知识点
推荐套卷
(本小题共12分）（注意:在试题卷上作答无效）
已知抛物线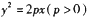上一动点P，抛物线内一点A(3,2) ,F为焦点且的最小值为.
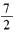(1)求抛物线的方程以及使得取最小值时的P点坐标；
(2)过（1)中的P点作两条互相垂直的直线与抛物线分别交于C、D两点，直线CD是否过一定点？若是，求出该定点的坐标,若不是，请说明理由.
粤公网安备 44130202000953号