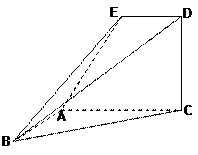（本小题满分12分）
如图，已知直角梯形ACDE所在的平面垂直于平面ABC，∠BAC＝∠ACD＝90O，∠EAC＝600，AB＝AC＝AE．
（1）在直线BC上是否存在一点P，使得DP∥平面EAB？请证明你的结论；
（2）求平面EBD与平面ABC所成的锐二面角
的大小。
相关试题
,
.
的解析式及周期
; 
时, 
,求
的值.
中，角
所对的边分别为
，
．
，
的值；
，求边AC的长。
的表达式，并求函数
，是否存在实数m，使函数
的值域恰为
？若存在，请求出m的取值；若不存在，请说明理由。
，
（I）求A的大小；（II）求
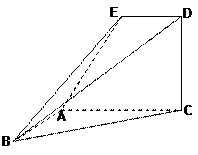
的值.推荐套卷
（本小题满分12分）
如图，已知直角梯形ACDE所在的平面垂直于平面ABC，∠BAC＝∠ACD＝90O，∠EAC＝600，AB＝AC＝AE．
（1）在直线BC上是否存在一点P，使得DP∥平面EAB？请证明你的结论；
（2）求平面EBD与平面ABC所成的锐二面角的大小。
粤公网安备 44130202000953号