．对于定义域为[
0，1]的函数f(x)，如果同时满足以下三条：①对任意的x∈[0,1] ，总有
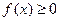；②f(1)=1；③若
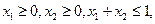都有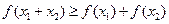
成立，则称函数f(x)为理想函数。
（1）若函数f(x)为理想函数，求f(0)的值；
（2）判断函数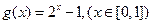
是否为理想函数，并予以证明。
，
，
，并猜想
，进一步归纳出更一般的结论
，
，
均为正数，且
+
+
在
处的切线与直线
垂直，求
的值
，使得
成立
，求
的最小值
满足
，求证
≥
时，等号成立相关知识点
推荐套卷
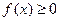．对于定义域为[0，1]的函数f(x)，如果同时满足以下三条：①对任意的x∈[0,1] ，总有；②f(1)=1；③若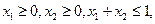都有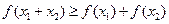成立，则称函数f(x)为理想函数。
（1）若函数f(x)为理想函数，求f(0)的值；
（2）判断函数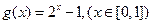是否为理想函数，并予以证明。
粤公网安备 44130202000953号