.(本题满分12分)
甲、乙两位学生参加数学竞赛培训.现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次,记录如下:
甲: 82 81 79 78 95 88 93 84
乙: 92 95 80 75 83 80 90 85
(1)画出甲、乙两位学生成绩的茎叶图,求出甲学生成绩的平均数以及乙学生成绩的中位数;
(2)若将频率视为概率,对甲学生在今后的三次数学竞赛成绩进行预测,记这三次成绩中高于80分的次数为 ,求
,求 的分布列及数学期望
的分布列及数学期望 .
.
相关知识点
推荐套卷
 中,底面ABCD是正方形,侧棱
中,底面ABCD是正方形,侧棱 底面ABCD,
底面ABCD, ,E是PC的中点,作
,E是PC的中点,作 交PB于点F.
交PB于点F.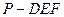 的体积.
的体积.
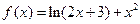 .
. 的单调性;
的单调性; 对任意
对任意 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.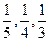 ,且他们是否破译出密码互不影响.
,且他们是否破译出密码互不影响.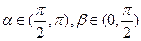 ,且
,且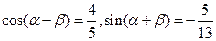 ,求
,求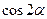 的值.
的值.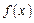 的定义域为R,当x<0时,
的定义域为R,当x<0时, .
.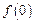 ,判断并证明函数
,判断并证明函数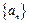 满足
满足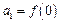 ,且
,且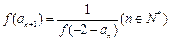 ,
,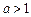 时,不等式
时,不等式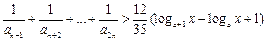 对不小于2的正整数
对不小于2的正整数 粤公网安备 44130202000953号
粤公网安备 44130202000953号