(本小题10分)
围建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,如图所示,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度为x米,总费用为y(单位:元).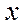
(1)将y表示为x的函数;
(2)试确定x,使修建此矩形场地围墙的总费用最小,
并求出最小总费用.
推荐套卷
 ,
,
 的最小正周期;
的最小正周期; ,求函数
,求函数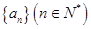 满足:
满足: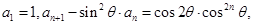 其中
其中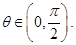
 时,求
时,求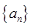 的通项公式;
的通项公式;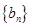 中,
中,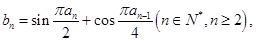 且
且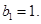 求证:对于
求证:对于 恒成立;
恒成立;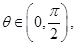 设
设 项和为
项和为 ,试比较
,试比较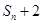 与
与 的大小.
的大小. 的一个焦点
的一个焦点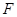 与抛物线
与抛物线 的焦点重合,P为椭圆与抛物线的一个公共点,且|PF|=2,倾斜角为
的焦点重合,P为椭圆与抛物线的一个公共点,且|PF|=2,倾斜角为 的直线
的直线 过点
过点 ,问抛物线
,问抛物线 上是否存在一点
上是否存在一点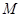 ,使得
,使得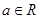 且
且 ,设函数
,设函数 = ax2 +x-3alnx.
= ax2 +x-3alnx.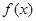 的单调区间;
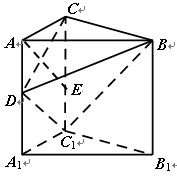
的单调区间;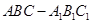 中,
中,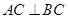 ,
,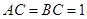 ,
,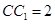 ,点
,点 、
、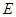 分别是
分别是 、
、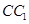 的中点.
的中点. 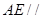 平面
平面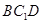 ;
; 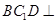 平面
平面 ;
;
 粤公网安备 44130202000953号
粤公网安备 44130202000953号