本小题满分12分)
假设一种机器在一个工作日内发生故障的概率为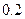 ,若一周5个工作日内无故障,则可获得利润10万元;仅有一个工作日发生故障可获得利润5万元; 仅有两个工作日发生故障不获利也不亏损;有三个或三个以上工作日发生故障就要亏损2万元.求:
,若一周5个工作日内无故障,则可获得利润10万元;仅有一个工作日发生故障可获得利润5万元; 仅有两个工作日发生故障不获利也不亏损;有三个或三个以上工作日发生故障就要亏损2万元.求:
(Ⅰ)一周5个工作日内恰有两个工作日发生故障的概率(保留两位有效数字);
(Ⅱ)一周5个工作日内利润的期望.
推荐套卷
本小题满分12分)
假设一种机器在一个工作日内发生故障的概率为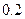 ,若一周5个工作日内无故障,则可获得利润10万元;仅有一个工作日发生故障可获得利润5万元; 仅有两个工作日发生故障不获利也不亏损;有三个或三个以上工作日发生故障就要亏损2万元.求:
,若一周5个工作日内无故障,则可获得利润10万元;仅有一个工作日发生故障可获得利润5万元; 仅有两个工作日发生故障不获利也不亏损;有三个或三个以上工作日发生故障就要亏损2万元.求:
(Ⅰ)一周5个工作日内恰有两个工作日发生故障的概率(保留两位有效数字);
(Ⅱ)一周5个工作日内利润的期望.