（本小题满分15分）
某企业有两个生产车间分别在A，B两个位置，A车间有100名员工，B车间有400名员工，现要在公路AC上找一点D，修一条公路BD，并在D处建一个食堂，使得所有员工均在此食堂用餐，已知A，B，C中任意两点间的距离均有1 km，设∠BDC＝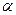
，所有员工从车间到食堂步行的总路程为S．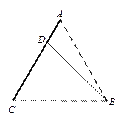
（1）写出S关于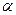的函数表达式，并指出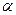的取值范围；
（2）问食堂D建在距离A多远时，可使总路程S最少？
相关试题
满足
,
．
是等比数列，并求出通项公式
；
设
是数列
的前
项和，求证：
．
中，平面
平面
，
为等边三角形，
且
，
，
分别为
，
的中点；
；
中，角
所对的边分别为
，且满足
．
的大小 ；
，求
中,
的二次函数的最小值为0，且有
，直线
的图象与
的图象交于两点，两点间的距离为
，数列
满足
．
是等比数列；
，求数列{
}的最小值及相应的
推荐套卷
（本小题满分15分）
某企业有两个生产车间分别在A，B两个位置，A车间有100名员工，B车间有400名员工，现要在公路AC上找一点D，修一条公路BD，并在D处建一个食堂，使得所有员工均在此食堂用餐，已知A，B，C中任意两点间的距离均有1 km，设∠BDC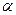＝，所有员工从车间到食堂步行的总路程为S．
（1）写出S关于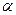的函数表达式，并指出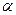的取值范围；
（2）问食堂D建在距离A多远时，可使总路程S最少？
粤公网安备 44130202000953号