抛掷三枚不同的具有正、反两面的金属制品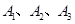
，假定
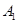正面向上的概率为
，
正面向上的概率为
，
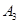正面向上的概率为t(0<t<1)，把这三枚金属制品各抛掷一次，设
表示正面向上的枚数。
(1)求的分布列及数学期望
(用t表示)；
(2)令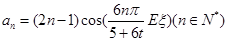
,求数列
的前n项和.
的前
项和为
，
．
，求数列
的前
．
中，角
所对的边分别为
，且满足
． 
的大小；
，求
的不等式
上定义运算*：
，若不等式
对任意
恒成立，求实数
的取值范围
的前
项和
．
的通项公式；
，求数列
的前推荐套卷
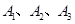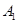抛掷三枚不同的具有正、反两面的金属制品，假定正面向上的概率为，正面向上的概率为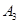，正面向上的概率为t(0<t<1)，把这三枚金属制品各抛掷一次，设表示正面向上的枚数。
(1)求的分布列及数学期望(用t表示)；
(2)令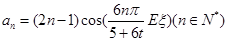,求数列的前n项和.
粤公网安备 44130202000953号