（本小题满分14分）
如图，四棱锥P-ABCD中，底面ABCD为菱形，且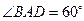
，侧面PAD是正三角形，其所在的平面垂直于底面ABCD，点G为AD的中点.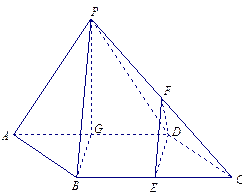
（1）求证：BG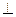
面PAD；
（2）E是BC的中点，在PC上求一点F，使得PG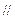
面DEF.
相关试题
中，
°，
，
平面
，
，设
的中点为
，
．
平面
；
的体积．
中，
分别是角
所对的边，且满足
．
的大小；
，求
的最小值．
．
；
，求实数
的值．
的方程为
，圆
的方程为
．
，其中
且m为常数．
时函数
在区间
上的单调性，并证明； 
在
处取得极值，求
的值，并讨论函数推荐套卷
（本小题满分14分）
如图，四棱锥P-ABCD中，底面ABCD为菱形，且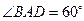，侧面PAD是正三角形，其所在的平面垂直于底面ABCD，点G为AD的中点.
（1）求证：BG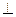面PAD；
（2）E是BC的中点，在PC上求一点F，使得PG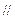面DEF.
粤公网安备 44130202000953号