（本小题满分15分）
在等比数列｛an｝中，首项为
，公比为
，
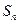表示其前n项和．
（I）记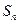=A，
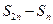= B，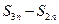
= C，证明A，B，C成等比数列；
（II）若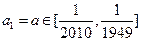
，
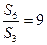，记数列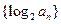
的前n项和为
，当n取何值时，有最小值．
相关知识点
推荐套卷
（本小题满分15分）
在等比数列｛an｝中，首项为，公比为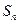，表示其前n项和．
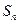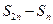（I）记=A，= B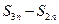，= C，证明A，B，C成等比数列；
（II）若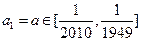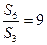，，记数列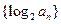的前n项和为，当n取何值时，有最小值．
粤公网安备 44130202000953号