(
某篮球联赛的总决赛在甲、乙两队之间角逐。采用七场四胜制,即有一队胜四场,则此队获胜,
同时比赛结束。在每场比赛中,两队获胜的概率相等。根据以往资料统计,每场比赛组织者可获
门票收入32万元,两队决出胜负后,问:
(1)组织者在此次决赛中,获门票收入为128万元的概率是多少?
(2)设组织者在此次决赛中获门票收入为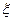 ,求
,求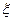 的分布列及
的分布列及 。
。
推荐套卷
(
某篮球联赛的总决赛在甲、乙两队之间角逐。采用七场四胜制,即有一队胜四场,则此队获胜,
同时比赛结束。在每场比赛中,两队获胜的概率相等。根据以往资料统计,每场比赛组织者可获
门票收入32万元,两队决出胜负后,问:
(1)组织者在此次决赛中,获门票收入为128万元的概率是多少?
(2)设组织者在此次决赛中获门票收入为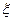 ,求
,求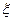 的分布列及
的分布列及 。
。