已知：在△ABC中，∠ACB=90°，CD⊥AB于点D，点E在AC上，BE交CD于点G，EF⊥BE交AB于点F．如图甲，当AC=BC，且CE=EA时，则有EF=EG；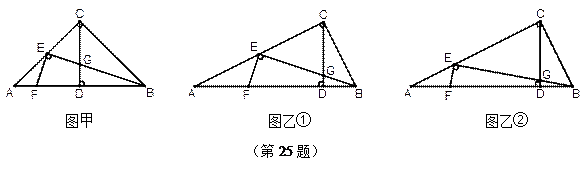
（1）如图乙①，当AC=2BC，且CE=EA时，则线段EF与EG的数量关系是：EF EG；
（2）如图乙②，当AC=2BC，且CE=2EA时，请探究线段EF与EG的数量关系，并证明你的结论；
（3）当AC=mBC，且CE=nEA时，请探究线段EF与EG的数量关系，直接写出你的结论（不必证明）．
．
，其中
，
．
中，AD⊥BC于点D，AD=BD，
=65°，求∠BAC的度数．
相关知识点
推荐套卷
粤公网安备 44130202000953号